Vocab

  • algorithmic efficiency: The ability of an algorithm to solve a problem in an efficient way
    • time complexity
    • space complexity
  • decision problem: a problem in computer science and mathematics that can be solved by a yes-no answer, also known as a binary answer. In other words, a decision problem is a problem for which there are only two possible outputs:"yes" or "no".
  • decidable problem: a problem in computer science and mathematics for which an algorithm can be created that can always produce a correct answer or solution
    • a problem for which there exists an algorithm that can be used to determine whether a given input is a valid solution or not
  • undecidable problem: problem in computer science and mathematics for which it is impossible to create an algorithm that can always provide a correct answer or solution
    • it is not possible for an algorithm to always determine whether a given input is a valid solution to an undecidable problem
  • the halting problem: an example of an undecidable problem. It states that it is not always possible to correctly determine whether a code halts or runs forever
    • There is no way to write an algorithm to analyze and determine whether a body of code can run forever or not.

3.17: Algorithm Efficiency

Purpose:

The purpose of this lesson is to help students understand how to make an efficient program and optimize it and understand its importance to the CSP curriculum.

What is Algorithmic Efficiency?

  • The ability of an algorithm to solve a problem in an efficient way
    • An efficient algorithm solves a problem quickly and with a minimum amount of resources, such as time and memory.
  • How do we determine if an algorithm is efficient or not?
    • One way we can do this is by determining the time complexity of the algorithm.
    • Another way is through space complexity.

Traveling Merchant Problem Hacks:

What did you and your team discuss? (record below)

  • An heuristic solution is an approach to a problem that produces a solution that isn't necessarily optimal but can be used when normal methods take forever

Describe the method used to solve the traveling merchant problem. (record below)

3.18: Undecidable Problems

Purpose:

The purpose of this lesson is to introduce students to the concept of undecidable problems in computer science and to explain why these problems are important.

Key vocabulary:

  • Decision problem
  • Decidable problem
  • Undecidable problem

Decision Problem

A decision problem is a problem in computer science and mathematics that can be solved by a yes-no answer, also known as a binary answer. In other words, a decision problem is a problem for which there are only two possible outputs:"yes" or "no". There are two types of decision problems that Collegeboard goes over:

  • Decidable Problems
  • Undecidable Problems

A decidable is a problem in computer science and mathematics for which an algorithm can be created that can always produce a correct answer or solution. In other words, a decidable problem is a problem for which there exists an algorithm that can be used to determine whether a given input is a valid solution or not.

An undecidable problem problem is a problem in computer science and mathematics for which it is impossible to create an algorithm that can always provide a correct answer or solution. This means that it is not possible for an algorithm to always determine whether a given input is a valid solution to an undecidable problem.

Decidable Problems

A decidable problem is an algorithm that can always have an output of yes or no given any input. It is always correct.

Example of a Decidable Problem

The procedure below tests to see if a number is divisible by 13. If it is, it returns true. If it isn't, it returns false.

def divideThirteen(number):
    if number % 13 == 0:
        return True
    else:
        return False

print(divideThirteen(26))
print(divideThirteen(30))

True
False

Undecidable Problems

An Example of a Forever Running Code

The code keeps adding 1 to the variable number until number is no longer an integer(This is not the python data type "integer", it's the integer in number theory). However, there is no end to this code, making the computer run forever. There is no halt to the code.

i = 0
number = 1
def integerTest(n):
    # Testing if the number is an integer
    if n%1 ==0:
        return True
    else:
        return False
# Using while loop to keep searching an a non-integer above 1. Note that the computer runs forever.
while i == 0:
    number += 1
    if integerTest(number) == False:
        i +=1
        print("Done")

The Halting Problem

The halting problem is an example of an undecidable problem. It states that it is not always possible to correctly determine whether a code halts or runs forever.

There is no way to write an algorithm to analyze and determine whether a body of code can run forever or not.

Halting Problem Example:

  • In order to understand this, suppose that an algorithm was able to analyze whether a code halts or not. Let's call this algorithm HaltChecker.
  • HaltChecker analyzes the program,program P, and its input,input I. If program P halts with input I, HaltChecker returns an output of "halts". If program P doesn't halt(runs forever) with input I, HaltChecker returns an output of "never". For example, in the code where it tests if variable number, the code runs forever, so HaltChecker returns an output of "never".
  • Then, we add another algorithm called Reverser which reverses HaltChecker's output. So, if "never" is the output of HaltChecker, then the output of Reverser is "halts". It's also the same the other way around: if HaltChecker has an output of "halts", then Reverser has an output of "never".
  • We combine these algorithms into one entire body of code.
  • Since Reverser is the algorithm at the end, hence giving the ultimate output, notice how it prints "never" when in fact there is an end(As proved by HaltChecker), and how it also prints "halts" when there is in fact is no end to the code(Also proved by HaltChecker). As a result, HaltChecker is inaccurate and this is an undecidable problem.

This Diagram Sums up the Entire Process in the Bulleted List:

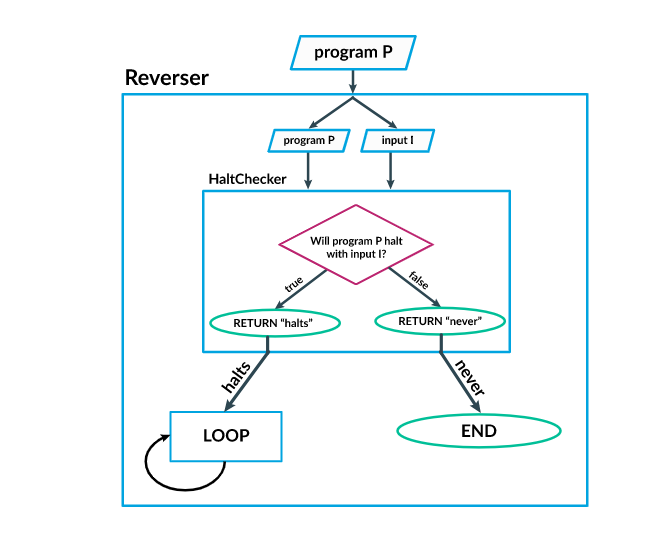
reverser

Credits of diagram and example to Khan Academy

FAQ

  • Q: If Reverser is causing the problem, why not remove it?
  • A: Removing Reverser will remove the problems, however, we are looking for ways which create the problem of not outputting a correct result. One example is enough to prove that it is an undecidable problem since it proves that the code is not completely accurate.

Extra Things to Notice

  • Note that while a computer may take a long time to run a section of code, it does not mean that the computer is going to run forever.
  • Humans are able to solve some undecidable problems. The entire Halting Problem example was to prove that computers cannot solve undecidable problems.